Latest qNMR experiments

There is a rapidly growing use of NMR for quantitation (qNMR) and its extension, mixtures analysis. [1] The experiment most commonly used for the purpose is a simple 1D ¹H spectrum. Whilst this suits many purposes, there are cases where this approach is insufficient or ambiguous, often as a consequence of signal overlap. This comes into sharper focus when targeted analysis is performed using mixtures of increasing complexity.

I will highlight here a few publications that point the way to some emerging technical advances that are relevant to extending the reach of targeted analysis using NMR.

1D NMR spectra of heteronuclei

It can be the case that a complex ¹H analysis can be simplified when another nucleus is observed, such as mixtures analysis using ¹³C{¹H} spectroscopy. [2] In fortunate cases ¹⁹F NMR (for example) may also be used to mitigate signal overlap and sometimes simplify a species to just one signal.

One critical consideration when making these experiments fully quantitative is to ensure that all resonances in the spectrum observe the same tip angle.

A ¹³C spectrum may cover 200 ppm, or 20 kHz using a 9.4 T system (¹H at 400 MHz). One rule-of-thumb is that the spectral width be < 1/(10*PW), so if PW=10 μs then the effective band width for quantitation is inadequate at about 10 kHz.  There is a long tradition of devising adiabatic pulses that have a large, uniform RF excitation band and good phase characteristics. One popular example of this is the CHIRP pulse. Recently Morris and co-workers described [3] the “CHORUS” pulse excitation scheme and its applicability to qNMR. CHORUS uses linear, phase-modulated, swept-frequency “chirp” pulses and is reported to have excellent excitation characteristics: “CHORUS achieves more than 99.9% excitation, with reproducibility better than 0.1%, over a bandwidth of more than 250 kHz”.

NMR data for quantitation using ¹³C, ¹⁹F observe or any nucleus that requires a wide excitation band should be acquired using a special excitation pulse rather than a standard hard pulse.

Fig. 1. ¹H NMR spectra recorded over a 300 kHz range with 99.9% excitation and excellent reproducibility.[3] This would also be very adequate for quantitative ¹³C and ¹⁹F NMR spectrum detection in a single experiment.

Solvent saturation

There are any number of solvent saturation pulse experiments to choose from, starting perhaps with the ubiquitous “noesypr1D”. The key is to achieve a hight level of solvent suppression, with minimum perturbation – saturation, phase-, or baseline distortion –  of nearby signals. Adding the “perfect echo” element to a pulse sequence appears to help considerably, and has been described for WATERGATE [4a] and W5 excitation sculpting [4b] .

High-dispersion NMR

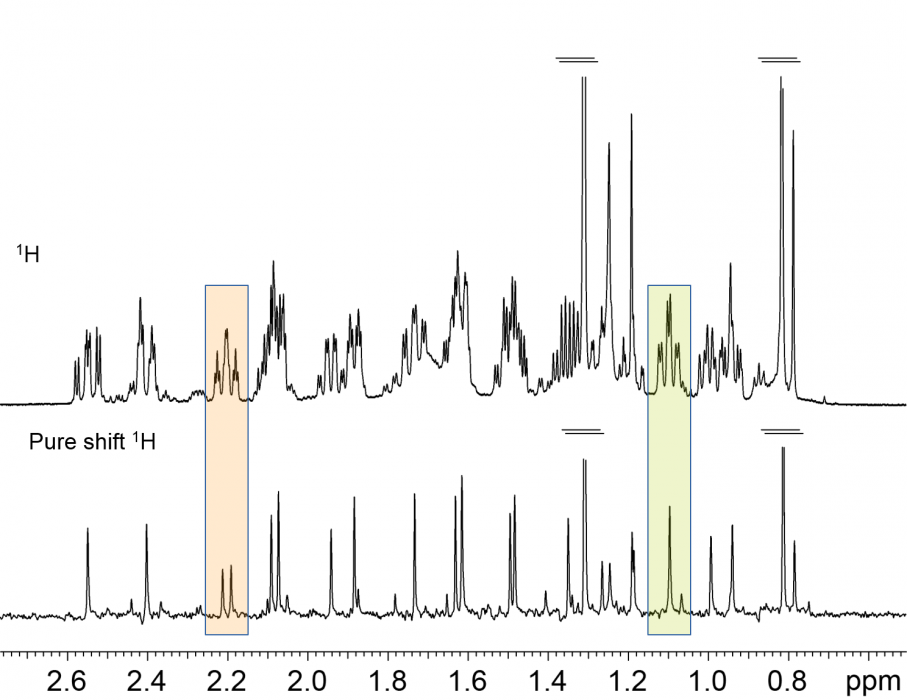
Another approach to effectively extend the applicability of ¹H NMR for targeted analysis is by reducing the peak overlap. So-called “Pure Shift” NMR experiments achieve this by “collapsing” all multiplets in a spectrum to a singlet [5]: the equivalent of a fully broad band ¹H decoupled spectrum is obtained. Whilst this prize does come at the cost of some loss in signal-to-noise sensitivity, the end result is highly desirable. In fact, Pure Shift experiments are starting to be used in everyday, routine NMR services to determine diastereomeric excesses, impurity levels, etc.
Its potential use for multicomponent mixture analysis using a targeted analytical approach is obvious.[6] Providing that the new “singlets” in the ¹H spectra can be confidently ascribed to a particular mixture component, the analysis will use the long-established, standard relationship of proportionality between normalised integrals and concentration.

Fig. 2 Conventional and Pure Shift ¹H NMR spectra of a reaction mixture. Note that some signals appear to be single multiplets, but the “fully ¹H decoupled” spectrum reveals them to be from different species.

2D NMR

The classical response to the overlap problem  in NMR is to increase the dimensionality of the experiment. It therefore stands to reason that 2D NMR can be used to reduce or eliminate signal overlap in 1H NMR spectra. Whilst the 1H multiplicity is retained, significant simplification is achieved. This fact has been exploited with a number of food mixtures, and Giradeau’s review article details the considerations for successful implementation.[1]
Whilst 2D homonuclear experiments can be of benefit, the greater utility is observed when 2D heterocorrelation experiments such as 2D ¹H-¹³C HSQC are employed. This has been described, for example, for extra virgin olive oil analysis [7] and heparin products [8].

Having your cake and eating it!

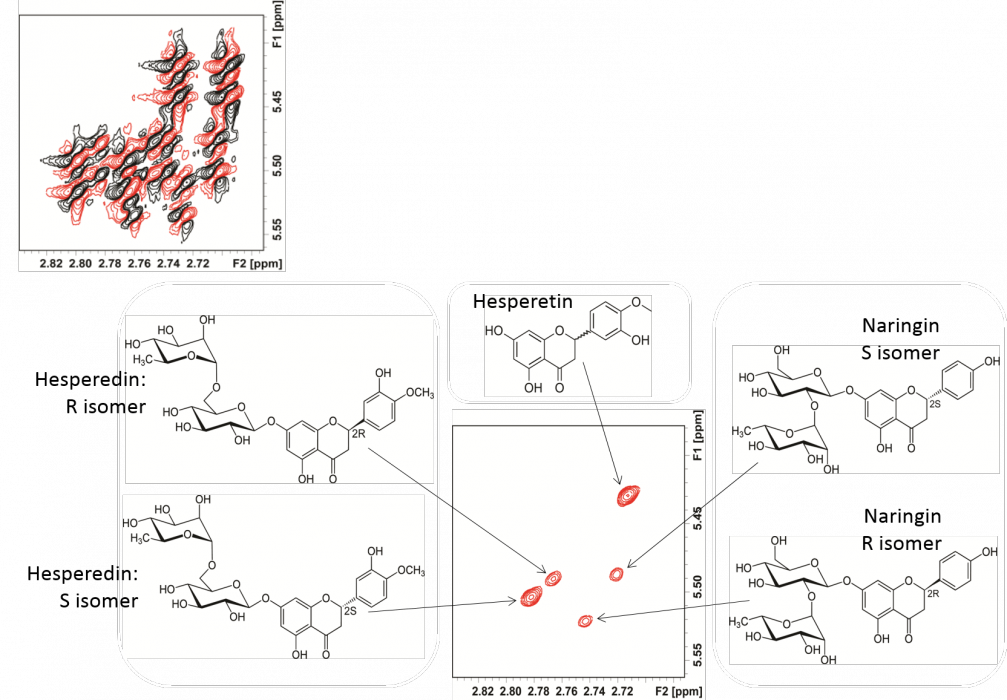
Whilst Pure Shift and 2D experiments have significant merit, what if we could combine the two experiments? The resulting 2D spectrum would ideally have a single peak for each of ¹H-¹³C partner because the ¹H multiplicity information is suppressed. [9]

Fig 3.  Pure-shift 2D COSY spectrum of a flavonoid mixture. In the upper left are the conventional, phase-sensitive 2D COSY cross peaks, having extensively overlapping cross peaks, and (lower contour plot) the effective separation of cross peaks for closely-related species. [6a]
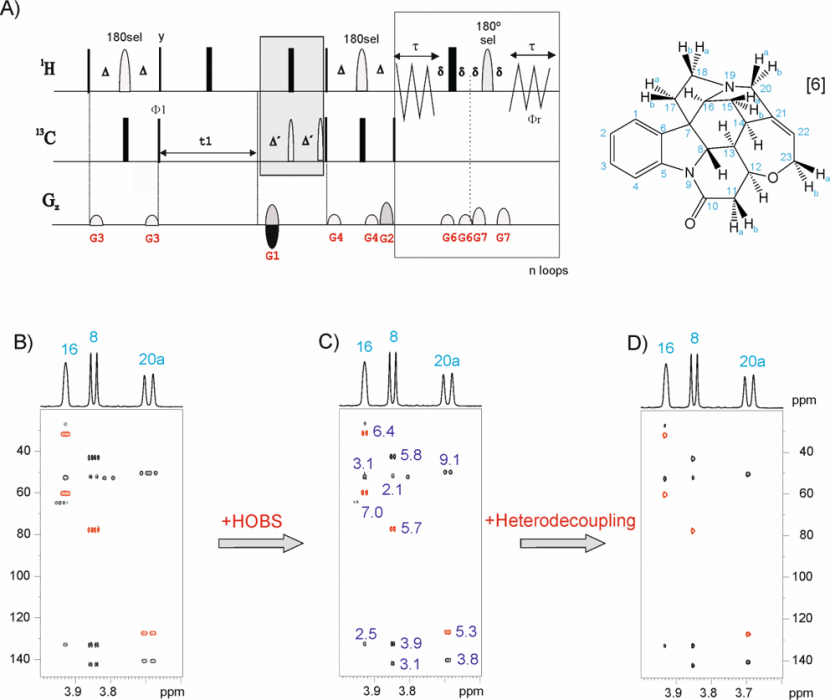
The Pure Shift 2D HSQC must offer the “ultimate” in resolution. A number of factors contribute towards a complication with this analysis: the “golden rule” of NMR quantitation is typically broken in that no single concentration proportionality factor can be applied to all 2D cross peaks to convert volumes to component concentration. This limitation may be a thing of the past as a result of work from Teo Parella’s laboratory in Barcelona, Spain. The family of so-called “Perfect” 2D HSQC experiments set out to produce NMR data ideally suited to quantitation.[9]

Fig 4. selHSQMBC experiment applied to brucine.

Data analysis

Mnova offers the Simple Mixtures Analysis (SMA) tool for targeted mixtures analysis. All of the experiments described in this article can be used as input for SMA– on their own, or as part of a number of qNMR experiments performed on a single, complex mixture. This will be demonstrated in a future article.

Acknowledgements

We thank Prof. Gareth Morris and co-workers, Manchester University, for advance information and figures on CHORUS (Fig. 1).
Dr Juan A. Aguivar-Malavia, Durham University, kindly provided images and data shown in Figs 2 and 3.
Dr Teo Parella provided Fig 5.

References

1. Giraudeau, P. Reson. Chem. 2014, 52 (6), 259–272.
2. Caytan, E.; Remaud, G. S.; Tenailleau, E.; Akoka, S. Talanta 2007, 71 (3), 1016–1021.
3. Power, J. E.; Foroozandeh, M; Adams, R. W.; Nilsson, M.; Coombes, S.; Phillips, A. R.; Morris, G. A. SMASH NMR Conference 2015, Bovena, Italy.
4. (a) Adams, R. W.; Holroyd, C. M.; Aguilar, J. A.; Nilsson, M.; Morris, G. A. Chem. Commun. (Camb). 2013, 49 (4), 358–360., (b) Aguilar, J. A; Kenright, S. J. Analyst 2015, in press. DOI: 10.1039/C5AN02121A
5. Castañar, L.; Parella, T. Magn. Reson. Chem. 2015, 53 (6), 399–426.
6. (a) Aguilar, J. A.; Morris, G. A.; Kenwright, A. M. RSC Adv. 2014, 4, 8278. (b) Aguilar, J. A.; Faulkner, S.; Nilsson, M.; Morris, G. A. Angew. Chemie Int. Ed. 2010, 49 (23), 3901–3903.
7. Dais, P.; Hatzakis, E. Anal. Chim. Acta 2013, 765, 1–27.
8. Keire, D. A.; Buhse, L. F.; al-Hakim, A. Anal. Methods 2013, 5 (12), 2984.
9. Castañar, L.; Parella, T. In Annual Reports on NMR Spectroscopy; 2015; Vol. 84, pp 163–232.